Feature Selection

Feature selection gives several options to select a subset of features from the original set of features.

The first option is to select the number of features you would like to keep in your dataset after feature selection. By default, EvoML determines the number of features to keep based on the dataset size, but you are able to set the number yourself. There is a balance to be struck as too many or too few features can affect the model's performance.

The second option is to select the feature selection method. By default, evoML uses MRMR Importance.

The next options are "Relevancy metric", "Redundancy metric", and "Redundancy aggregation". If your feature selection method is MRMR or MRMR Importance, you can provide metrics to use here. To know more about these metrics anf how they are used, please see the MRMR concept.

If you have selected the Filter method, the metrics options will remain but they will be used for a two-stage filter. The first stage will filter out features based on the relevancy metric, and the second stage will filter out features based on the redundancy metric (notice that this is different from MRMR which is an iterative algorithm).

If you are using Feature Importance (either as metric or if you are using MRMR Importance) you will be able to select the models and aggregation method to use for feature importance.

Finally, if you are using MRMR you are going to be presented with additional options for it. The "Linear" setting (off by default) simply denotes whether the relevancy will be divided by redundancy or if subtraction will be used. You are also going to be presented with "Redundancy Weight" option, which is the weight with respect to relevancy. Essentially, a higher score puts more value on correlation between features and a lower score puts more value on correlation with target.

Feature Selection

Data may contain a large amount of features, most likely some of them may be irrelevant or redundant. Feature selection is the process of selecting a subset of relevant features for use in model construction. Feature selection techniques are used for several reasons:

• Simplification of models to make them easier to interpret
• Shorter training times
• Better performance due to noise reduction

EvoML uses MRMR (Minimum Redundancy Maximum Relevance) as its main feature selection framework.

MRMR (Minimum Redundancy Maximum Relevance)

What is MRMR?

MRMR is a method that selects features based on their relevance to the target variable and their redundancy with other features. Let's consider a simple example, say that our goal is to predict house prices and we know some of the features:

So we have 6 features, and let's say that we want to reduce this down to 3 best features. Standard feature selection methods would select the 3 features that are most relevant to the target feature. However, MRMR would select the 3 features that are most relevant to the target feature and least redundant with each other. What does this mean?

We can use various correlation techniques to measure the relevancy of features with respect to the target to see which features have stronger predictive power:

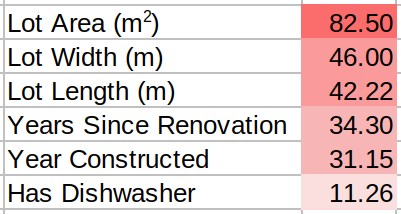
From the figure above, we can see that "Lot Area", "Lot Width", and "Lot Length" have the highest correlation with the target feature "Price". However, as you may have noticed, these three features are very similar and possibly correlate with each other. In fact, we know that most likely "Lot Area" is simply "Lot Width" multiplied by "Lot Length".

Please note that "Lot Length" and "Lot Width" are not redundant on their own (hence the high correlation score), but if we already picked "Lot Area", then adding width and length features becomes redundant.

This is exactly the problem with many feature selection techniques: they provide individual evaluation for each feature.

So how does MRMR work?

MRMR is an iterative algorithm where at each iteration it identifies a single best feature and adds it to a list of selected features. This list is populated until N best features were found (where N is a parameter, in our case we set it to 3).

And how does MRMR decide which feature is the best? As you may recall MRMR stands for "Maximum Relevance Minimum Redundancy", and it is called so because at each iteration the algorithm tries to find a balance between how relevant a feature is to the target, and how redundant it is with respect to features that were previously selected as best features.

There are many variants of MRMR, the "standard" one is where F-Test is used to compute relevance, is used to compute the Redundancy, the redundancy is aggregated using mean average, and then Relevance is divided by aggregated Redundancy to get the final score.

Pearson Correlation

Let's see how MRMR would select features from our example:

Iteration 1: Our goal is to select 3 features. We don't have any features selected yet, so we will simply use the relevance score to select the best feature. This is equivalent to selecting the top feature from Figure 2. So in our case, MRMR would select "Lot Area".

Iteration 2: We have "Lot Area" as a selected feature, we need two more. Relevancy (Figure 2) is already computed, let's compute the Redundancy:

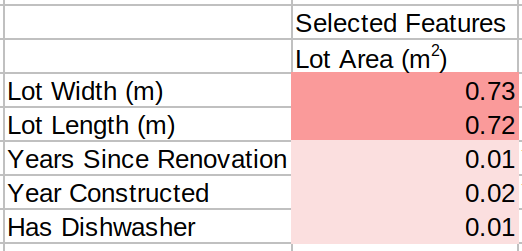
And now we divide Relevancy by Redundancy to get the final score:

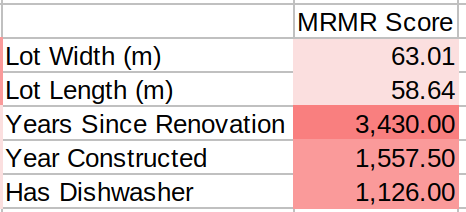
The "Years Since Renovation" feature has the highest score, so it is selected as the best feature and added to the list of selected features.

Note that "Lot Width" and "Lot Length" got low MRMR score as they have high correlation with "Lot Area" which was already selected, making them redundant.

Iteration 3: Our list of best features contains "Lot Area" and "Years Since Renovation". We need one more feature. Let's repeat the process of calculating redundancy and dividing Relevancy by Redundancy:

(Please note that we computed the average Redundancy for each feature, as now we have more than 1 best feature selected from previous iterations)

"Has Dishwasher" got the highest score, hence it is selected as the best feature and added to the list of selected features. We found our 3 best features! Let's summarise what happened:

1. On our first iteration Lot Area was selected as this feature has highest correlation with the target (which is Price).
2. On the second iteration "Years Since Renovation" was selected (Lot Length and Width got lower scores as they are highly correlated with Lot Area that was selected in the previous iteration).
3. On the third iteration "Has Dishwasher" was selected. Note that although this feature has the lowest correlation with the target, other features have strong relationship with best features that we selected in previous iterations, making them more redundant.

MRMR in EvoML

There are different variations of MRMR, but they follow the same principle - we compute relevancy between features and the target, compute redundancy between all features that we are selecting from and features we have selected as "best" in previous iterations, aggregate redundancy, and finally compute MRMR scores. The difference between various MRMR approaches is one of these three:

• A different metric used for either Relevancy and/or Redundancy
• A different way of aggregating Redundancy (usually either mean average or selecting the largest value)
• A different way of computing the final score (two options here - division or subtraction)

EvoML uses F-Test for Relevancy, Pearson for Redundancy, mean average for aggregation, and division by default as this method is considered as the "standard" MRMR, it has a great balance between accuracy and time it taken for computation. However, you are not limited to these options and can try changing them when setting up a trial:

MRMR Importance

This is the default feature selection method in EvoML.

This algorithm works in two stages:

1. 90% of the features are selected using MRMR
2. The remaining 10% of the features are selected using feature importance

Our internal experimentation has shown that combining MRMR with feature importance gives the best results, better than using either of these methods on their own.